はじめに
今回は、勾配ブースティング決定木(Gradient Boosting Decision Tree, GBDT)を用いて、マーケティング施策を選定する枠組みについて解説します。具体的には、説明変数]から目的変数
を予測するモデルを構築し、各説明変数の重要度を算出することで、どの説明変数がマーケティング施策の対象になり得るかを検討します。
例えばとして製品のステータス、
を製品の打ち上げとすると、製品のステータスのうち、どの要素が売上に貢献しているか示唆する情報が得られます。この情報を利用することで「どの要素に注力して売り出すか」「どの要素に注力して改善を目指すか」など、適切な施策の選定につながります。
勾配ブースティング決定木とは
勾配ブースティング決定木は、単純な「決定木」というモデルを拡張した、高精度かつ高速な予測モデルです。
理論の全体像については、以下のブログ記事がとても良くまとまっていました。本記事では、マーケティング施策の選定に活かすという観点で必要な部分のみを概観します。
http://hiyoko9t.hatenadiary.jp/entry/2017/12/03/204333hiyoko9t.hatenadiary.jp
決定木とは
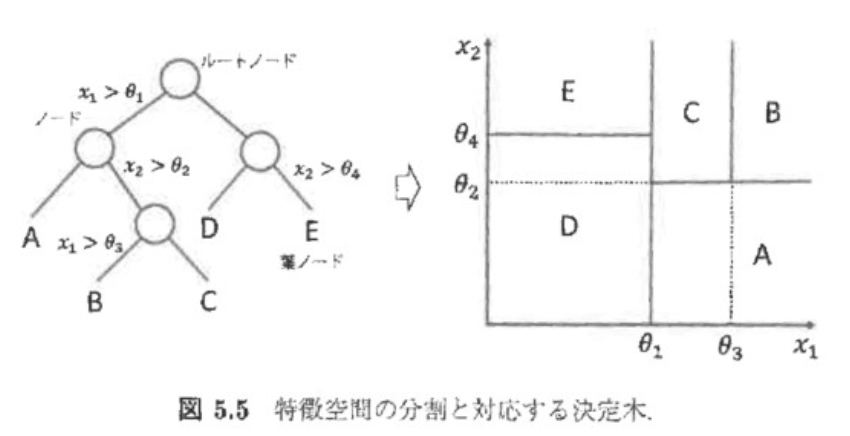
決定木とは、のとある要素に対して次々と分岐点を見つけていくことで
を分類しようとするモデルです。視覚的にも結果が理解しやすいという利点があります。
アンサンブルとは
アンサンブルとは、決定木のような単純なモデルを複数組み合わせ、複雑で非線形なモデルを構築する手法です。個々のモデルは単純なため高速に実行できるにもかかわらず、「3人よれば文殊の知恵」ということで高い精度も実現できる枠組みとされています。
代表的な手法としては、以下の二つが挙げられます。
- バギング
- ブースティング
決定木を「バギング」で拡張したモデルの一つに「ランダムフォレスト」があります。そして「ブースティング」で拡張したモデルが、勾配ブースティング決定木です。
バギング
バギングは、訓練データから重複を許して何度もデータセットを作成し、それぞれで学習した複数のモデルの結果を利用する手法です。「訓練データから重複を許して何度もデータセットを作成」するのは「ブートストラップ法」と呼ばれています。

ブースティング
バギングはデータセットを複数個作り、それぞれ独立で学習させています。そのため、せっかく何回も学習しているのに、過去の間違いを「反省」して次のモデル構築に活かせていません。
ブースティングは、先に学習したモデルで分類に失敗した訓練データを積極的に分類できるよう、後段のモデルを修正していく手法です。逐次的にモデルを作成し、最終的には個々のモデルの精度を用いた重み付き多数決を実施します。

ここまで説明したように「勾配ブースティング」は「決定木」という「のとある要素に対して次々と分岐点を見つけていくことで
を分類しようとするモデル」を、過去の失敗を活かすように複数作成していくモデルです。
決定木がベースになっているので、最終的にはのどの要素での分岐が
の予測に寄与しているか、つまりは各説明変数の重要度を算出できるモデルとなっています。
Pythonでの実装例
最後に以下では、有名なirisのデータセットを用いたPython実装例を示します。を花の情報、
を花の種類としています。
実装例は、GitHubでも公開しています。
github.com
データの準備
import pandas as pd import numpy as np from sklearn.datasets import load_iris iris_dataset = load_iris() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(iris_dataset['data'], iris_dataset['target'], test_size=0.1, random_state=0)
データの可視化
X_trainの次元を削減して、花の種類で色分けしてみます。現実のデータだと、ここまで綺麗に分かれていることは無いかと思います。
%matplotlib inline import matplotlib.pyplot as plt from sklearn.manifold import TSNE X_reduced = TSNE(n_components=2, random_state=0).fit_transform(X_train) plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y_train)

モデルの構築(クロスバリデーション)
from sklearn.model_selection import GridSearchCV from sklearn.ensemble import GradientBoostingClassifier learning_rate = [0.05, 0.1, 0.02] max_depth = [2, 3, 4] min_samples_leaf = [5, 9, 17] max_features = [1.0, 0.3, 0.1] hyperparams = {'learning_rate': learning_rate, 'max_depth': max_depth, 'min_samples_leaf': min_samples_leaf, 'max_features': max_features} gd = GridSearchCV(estimator = GradientBoostingClassifier(n_estimators=30), param_grid = hyperparams, verbose=True, cv=10, scoring = "accuracy", n_jobs=10) gd.fit(X_train, y_train) print(gd.best_score_) print(gd.best_estimator_)
クロスバリデーションの結果、以下の結果が得られました。
0.9703703703703703
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.05, loss='deviance', max_depth=4,
max_features=0.1, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=17, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=30,
presort='auto', random_state=None, subsample=1.0, verbose=0,
warm_start=False)
テストデータに適用
構築した予測モデルをテストデータに適用したところ、全て的中しました。
from sklearn.metrics import confusion_matrix clf = gd.best_estimator_ clf.fit(X_train, y_train) confusion_matrix(y_test, clf.predict(X_test))
array([[3, 0, 0],
[0, 8, 0],
[0, 0, 4]], dtype=int64)
説明変数の重要度の算出
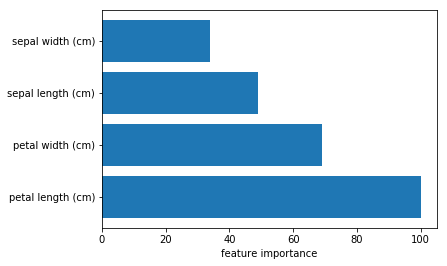
説明変数の重要度を可視化した結果を、以下に示します。petal lengthが一番重要で、sepal widthが一番重要でないと分かります。
今回の場合は説明変数が四つしかないこともあり「だから何?」という印象も受けますが、説明変数が膨大な場合などでも重要な要素を機械的に選定できる点で価値がある手法です。
feature_importance = clf.feature_importances_ feature_importance = 100.0 * (feature_importance / feature_importance.max()) label = iris_dataset.feature_names plt.xlabel('feature importance') plt.barh(label,feature_importance, tick_label=label, align="center")