主成分分析における行列表現

線形次元削減

　高次元の訓練入力標本から低次元の表現を求めること。
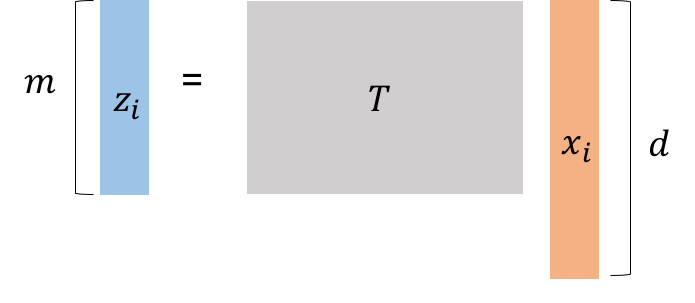
　つまりの埋め込み行列を用いて、としてを求めること。

主成分分析

　次元削減後の表現がの正射影であるという制約の下で、がとなるべく近くなる埋め込み行列を決定する。
　下線部はと行列を用いて表現できる。
　このときとは次元が違うので、単純に比較できない。そのために左からをかけてとして次元を揃える。
　これらの差を最小化するようなを求めることになる。